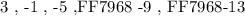We will take a look at how we go about with arithmatic progressions.
Arithmmetic sequences are caetgorized by the following two parameters:
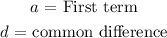
Where,
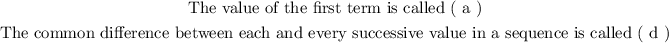
We are given the following arithmetic sequence:
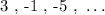
Now we will try to determine the values of the two parameters ( a and d ) from the given sequence as follows:
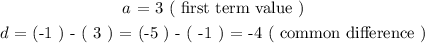
Now to determine the value of any term number ( n ) in an arithmetic sequence we use the following formula:
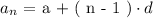
Where,
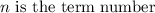
So if we plug in the values of arithmetic sequence parameters into the general equation above we get:
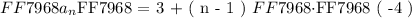
Now we are to determine the values of term numbers ( n = 4 ) and ( n = 5 ). We will evaluate the ( an ) for each term number as follows:
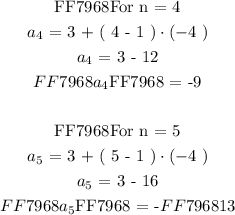
Hence, the next two consecutive numbers in the arithmetic sequence would be: