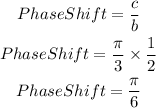Question

Amplitude, period, and phase shift of sine and cosine functions

Answer 1

We are given that

`y=-2+2\cos (2x-(\pi)/(3))`

Note: Given the cosine function

`y=a\cos (bx-c)+d`

then

`\begin{gathered} Amplitude=a \\ Period=(2\pi)/(b) \\ PhaseShift=(c)/(b) \\ VerticalShift=d \end{gathered}`

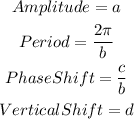
Comparing the question with what is written in the note

We have

`\begin{gathered} a=2 \\ b=2 \\ c=(\pi)/(3) \\ d=-2 \end{gathered}`

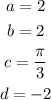
We want to find

(a). Amplitude

From the given question, the amplitude (a) is

`\begin{gathered} a=2 \\ Amplitude=2 \end{gathered}`

(b).Period

From the given question, the period is

`\begin{gathered} Period=(2\pi)/(b) \\ Period=(2\pi)/(2) \\ Period=\pi \end{gathered}`

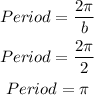
(c). Phase Shift

From the given question, the phase shift is

`\begin{gathered} PhaseShift=(c)/(b) \\ PhaseShift=(\pi)/(3)*(1)/(2) \\ PhaseShift=(\pi)/(6) \end{gathered}`