Given:
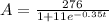
Where A is the number of deer expected in the herd after t years.
We will find the following:
(a) How many deer will be present after 3 years?
So, substitute t = 3 into the given equation:
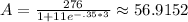
Rounding to the nearest whole number
So, the answer will be A = 57
=========================================================
(b) How many years will it take for the herd to grow to 50 deer?
substitute A = 50 then solve for t
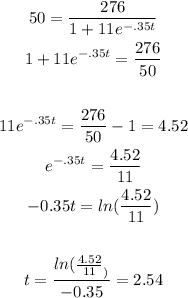
Round your answer to the nearest whole number.
So, the answer will be t = 3