Question

How many solutions can be found for the system of linear equations represented

on the graph?
A) no solution
3) one solution
D) infinitely many solutions
C) two solutions

Answer 1

Infinitely Many Solutions

Explanation:

They are the same line so they cross each other infinitely many times.

If you picked a point on the first equation it would be the same point on the second equation.

Answer 2

D) Infinitely many solutions

Explanation:

Given the follwowing systems of linear equations, y = x + 2, and -3x + 3y = 6:

Transforming -3x + 3y = 6 into its slope-intercept form, y = mx + b:

-3x + 3y = 6

Add 3x to both sides:

-3x + 3x + 3y = 3x + 6

3y = 3x + 6

Divide both sides by 3:

`(3y)/(3) = (3x + 6)/(3)`

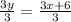
y = x + 2 ⇒ This is the slope-intercept form of -3x + 3y = 6. Since they are equivalent equations, then it means that their graphed lines coincide. Since any point on either lines coincide (or also exists) on the other line, then it means that the solutions to one of the equations will satisfy the other. Therefore, the given systems of linear equations have an infinitely many solutions.