Question

Two identical clocks are set to 12 noon time when on the ground at rest relative to the ground. One clock is placed in a spacecraft, sent into space and accelerated to a speed of v = 0.93 x 108 m/s. What will the moving clock read if the first clock reads 6 p.m.? Express your answer as the number of minutes from 6 pm.

Answer 1

First, for this problem, we will need to know the formula for time dilation

`t=\frac{t_0}{\sqrt{1-(v^2)/(c^2)}}`

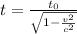
Where t is the time in the reference frame on earth

t0 is the time on the ship

v is the velocity relative to lightspeed

and c is light speed in a vacuum

For this problem, we will need to convert .93x10^8 to a fraction of light speed.

.93x10^8 = .31c

Now, we can plug in the numbers we get from the given

t0 = 6 hours since the ship has been in the air for 6 hours

`t=\frac{6}{\sqrt{1-((.31c)^2)/(c^2)}}`

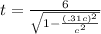
t = 6.31089

For the answer to be valid, we will convert .31089 to minutes by multiplying it by 60 (60 minutes in a hour)

18.654 minutes