Question

A sample of 25 measurements at breaking strength of cotton thread gave a mean of 7.4 and a standard deviation of 1.2 gms. Find 95% confidence limits for the mean breaking strength of cotton thread.

Answer 1

(6.9296, 7.8704)

Explanation:

Given:

• Sample Mean = 7.4

,

• Sample Standard Deviation = 1.2

,

• n = 25

First, determine the standard error.

`S.E.=(\sigma)/(√(n))=(1.2)/(√(25))=(1.2)/(5)=0.24`

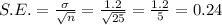
At 95% confidence limits, Z=1.96.

Using the formula below:

`\bar{x}-Z_{(\alpha)/(2)}(S.E)<\mu<\bar{x}+Z_{(\alpha)/(2)}(S.E)`

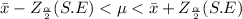
The limits is calculated below:

`\begin{gathered} 7.4-(1.96*0.24)<\mu<7.4+(1.96*0.24) \\ 7.4-0.4704<\mu<7.4+0.4704 \\ 6.9296<\mu<7.8704 \end{gathered}`

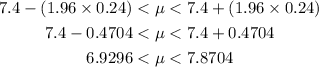
At 95%, the confidence limits for the mean breaking strength of cotton thread is (6.9296, 7.8704).