SOLUTION
The following diagram will help us solve the problem
(a) From the diagram, the height of the parallelogram is given as TR, and it is 40 mm
Now we can use the area which is given to us as 3,600 square-mm to find the base of the parallelogram, which is PQ
So,

Hence PQ is 90 mm
(b) Now, note that the side
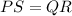
So, we will find QR
Also, since we have PQ, we can find TQ, that is
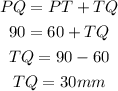
Note that triangle QRT is a right-angle triangle, and QR is the hypotenuse or the longest side
From pythagoras
So,
![\begin{gathered} QR^2=TR^2+TQ^2 \\ QR^2=40^2+30^2 \\ QR^2=1600+900 \\ QR^2=2,500 \\ QR=\sqrt[]{2,500} \\ QR=50mm \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rjkkmdv1ohgbxdj9lq1g7alyihc35ownva.png)
Now, since
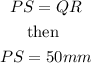
Hence PS is 50 mm