Question

The height of a pole is 15 feet. A line with banners is connected to the top of the poleto a point that is 8 feet from the base of the pole on the ground. How long would theline with banners need to be in order for the pole to be at a 90° angle with the ground?Explain your reasoning.

Answer 1

In order to have a 90º angle (right angle) the length of the line with banners needs to fullfit the Pythagorean theorem: In a right triangle the squared hypotenuse is equal to the sum of the legs squared:

`h^2=l^2+l^2`

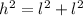
In the given situation the hypotenusa is the line with banners, and the legs are the pole and the 8ft ground from the base of the pole to the end of the line with banners:

h= x

l= 15ft

l= 8ft

`x^2=(15ft)^2+(8ft)^2`

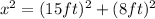
Solve the equation to find the value of x:

`\begin{gathered} x^2=225ft^2+64ft^2 \\ x^2=289ft^2 \\ x=\sqrt[]{289ft^2} \\ x=17ft \end{gathered}`Then, to make a right triangle the length of the line witg banners need to be 17ft