Question

A motor scooter travels 22 mi in the same time that a bicycle covers 8 mi. If the rate of the scooter is 6 mph more than twice the rate of the bicycle, find both rates.The scooter’s rate is ____ mph. (Type an integer or a decimal)

Answer 1

Let's use the variable x to represent the speed of the scooter and y to represent the speed of the bicycle.

For a same time t, the scooter travels 22 mi and the bicycle travels 8 mi, so we can write the following equation:

`\begin{gathered} distance=speed\cdot time\\ \\ 22=x\cdot t\\ \\ t=(22)/(x)\\ \\ 8=y\cdot t\\ \\ t=(8)/(y)\\ \\ (22)/(x)=(8)/(y) \end{gathered}`

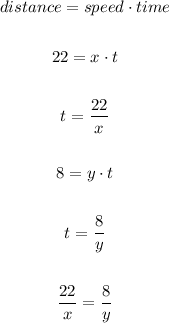
Then, if the rate of the scooter is 6 mph more than twice the rate of the bicycle, we have the following equation:

`x=2y+6\\`

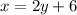
Using this value of x in the first equation, let's solve it for y:

`\begin{gathered} (22)/(2y+6)=(8)/(y)\\ \\ 22y=8(2y+6)\\ \\ 22y=16y+48\\ \\ 6y=48\\ \\ y=8\text{ mph} \end{gathered}`

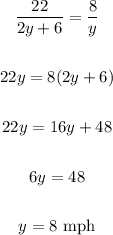
Now, calculating the value of x, we have:

`\begin{gathered} x=2y+6\\ \\ x=16+6\\ \\ x=22\text{ mph} \end{gathered}`

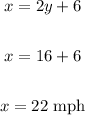
Therefore the scooter's rate is 22 mph and the bicycle's rate is 8 mph.