Answer:
a) 5 m
b) 0.667 s
c) 0.5 m
d) 0.75 m/s
e) -5 m
Step-by-step explanation:
In an equation of the form
y(x, t) = Acos(kx - ωt)
A is the amplitude, ω = 2π/T where T is the period, and k = 2π/λ where λ is the wavelength. In this case, the equation os
y(x,t) = 5cos(π(4x - 3t)
y(x,t) = 5cos(4πx - 3πt)
So, A = 5, k = 4π, and ω = 3π. Then, we can find each part as follows
a) Amplitude
The amplitude is A, so it is 5 m.
b) the period
Using the equation ω = 2π/T and solving for T, we get:
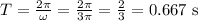
So, the period is 0.667 s
c) the wavelength.
using the equation k = 2π/λ and solving for λ, we get:
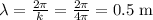
So, the wavelength is 0.5 m
d) The wave speed
The wave speed can be calculated as the division of the wavelength by the period, so
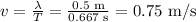
e) The height of the wave at (2, 1)
To find the height, we need to replace (x, t) = (2, 1) on the initial equation, so
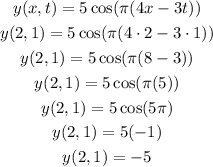
Then, the height of the wave is -5 m.
Therefore, the answers are
a) 5 m
b) 0.667 s
c) 0.5 m
d) 0.75 m/s
e) -5 m