Question

What are the possible values for the missing term of the geometric sequence? .004, _____, .4.04.04, -.04.0004.0004, -.0004

Answer 1

By definition, in a Geometric sequence the terms are found by multiplying the previous one by a constant. This constant is called "Common ratio".

In this case, you know these values of the set:

`\begin{gathered} .004 \\ .4 \end{gathered}`

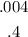
Notice that you can set up this set with the value given in the first option:

`.004,.04,.4`

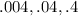
Now you can check it there is a Common ratio:

`\begin{gathered} (0.04)/(0.004)=10 \\ \\ (.4)/(0.04)=10 \end{gathered}`

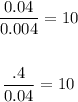
The Common ratio is:

`r=10`

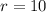
Therefore, it is a Geometric sequence.

Apply the same procedure with each option given in the exercise:

- Using

`.004,.04,-.04,.4`

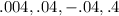
You can notice that it is not a Geometric sequence, because:

`\begin{gathered} (-.04)/(.04)=-1 \\ \\ (.4)/(-.04)=-10 \end{gathered}`

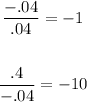
- Using

`.004,.0004,.4`
`\begin{gathered} (.0004)/(.004)=0.1 \\ \\ (4)/(.0004)=1,000 \end{gathered}`

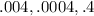
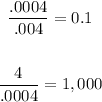
Since there is no Common ratio, if you use the value given in the third option, you don't get a Geometric sequence.

- Using this set with the values given in the last option:

`.004,.0004,-.0004,.4`

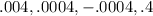
You get:

`\begin{gathered} (.0004)/(.004)=0.1 \\ \\ (-.0004)/(.0004)=-1 \end{gathered}`

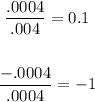
It is not a Geometric sequence.

The answer is: First option.