Question

Can I get help, the last tutor didn't help me that much.

Answer 1

We know that

• The volume of one ball is 221 cubic centimeters.

Since the ball is spherical, we can find its radius with the following formula.

`\begin{gathered} V=(4)/(3)\pi r^3 \\ 221\cdot(3)/(4\pi)=r^3 \\ r^3=(663)/(4\pi) \\ r=\sqrt[3]{(663)/(4\pi)}\approx3.75 \end{gathered}`

The diameter would be double than the radius, by definition.

`d=2(3.75)=7.5`

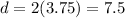
Since there are three balls in the cylinder, the height would be

`h=3(7.5)=22.5`

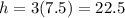
Now, we find the volume of the cylindrical package.

`V=\pi r^2h=\pi(3.75)^2(22.5)\approx993.52`

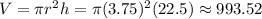
Therefore, the volume of the cylindrical package is 993.52, approximately.