Question

Describe the transformation of f(x) that produce g(x). f(x)= 2x; g(x)= 2x/3+7Choose the correct answer below.

Answer 1

To produce g(x) from f(x), we perform the transformation of dividing f(x) by 3 and adding 7.

Step-by-step explanation:

To transform f(x) to g(x), we need to perform two operations: division by 3 and addition of 7.

1. First, divide f(x) by 3: g(x) = f(x)/3 = 2x/3
2. Next, add 7 to the result: g(x) = 2x/3 + 7

Therefore, to produce g(x) from f(x), we perform the transformation of dividing f(x) by 3 and adding 7.

Answer 2

`\begin{gathered} f(x)=2x \\ g(x)=(2)/(3)x+7 \end{gathered}`

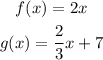
The vertical translation involves shifting the graph either up or down on the y axis. For example.

`\begin{gathered} y=f(x) \\ \text{translated upward }it\text{ will be } \\ y=f(x)+k \end{gathered}`

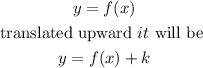
When a graph is vertically compressed by a scale factor of 1/3, the graph is also compressed by that scale factor. This implies vertical compression occurs when the function is multiplied by the scale factor. Therefore,

`\begin{gathered} f(x)=2x \\ \text{The vertical compression by a scale of }(1)/(3)\text{ will be} \\ g(x)=(1)/(3)(2x)=(2)/(3)x \end{gathered}`

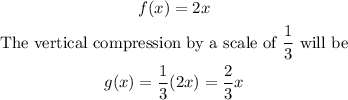
Finally, the vertical translation up 7 units will be as follows

`g(x)=(2)/(3)x+7`

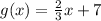
The answer is a. There is a vertical compression by a factor of 1/3 . Then there is a vertical translation up 7 units.