STEP - BY - STEP EXPLANATION
What to find?
The average rate of change in the height, in feet per second, during the first 1.25 seconds that the beach ball is in the air.
Given:
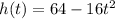
Step 1
Differentiate the heigh with reospect to t.
The rate of change of height is the differentiation of the height.
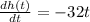
Step 2
Substitute t= 1.25

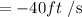
ANSWER
Average rate = -40 ft / s