Question

25.0 mL of a solution with concentration 0.30 M is diluted to a final volume of 150. mL. What is the final concentration?

Answer 1

Answer: the concentration of the solution after the dllution is 0.050 M

Step-by-step explanation:

The question requires us to determine the concentration of a solution after a dilution process.

The following information was provided by the question:

Concentration of initial solution = C1 = 0.30 M

Volume taken from initial solution = V1 = 25.0 mL

Volume of final solution = V2 = 150 mL

When a solution is diluted, the number of moles of the substance remains the same. Thus, we can say that:

`n_1=n_2`

where (1) is the solution before dilution and (2) refers to the solution after dilution.

The number of moles of a substance can be obtained from the definition of molarity (or molar concentration), where the number of moles is divided by the volume of the solution:

`molarity=\frac{number\text{ of moles}}{volume}\rightarrow number\text{ of moles = molarity}* volume\rightarrow n=C* V`

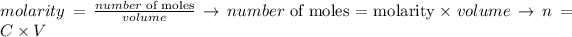
Thus, we can write that for a dillution:

`n_1=n_2\rightarrow C_1* V_1=C_2* V_2`

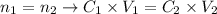
From the expression above we can determine the concentration of the final solution. Applying the values provided by the question to the expression above, we'll have:

`\begin{gathered} \begin{equation*} C_1* V_1=C_2* V_2 \end{equation*} \\ \\ (0.30M)*(25.0mL)=C_2*(150mL) \\ \\ C_2=((0.30M)*(25.0mL))/((150mL))=0.050M \end{gathered}`

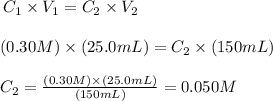
Therefore, the concentration of the solution after the dilution is 0.050 M.