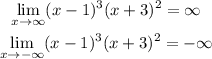Question

Can you please help me with 44Please use all 3 forms of the expression such as : down/up. As _,_ And limits

Answer 1

`\begin{gathered} x-\text{intercept}=-3\text{ and 1} \\ y-\text{intercept}=\text{ -9} \end{gathered}`
`\begin{gathered} x=1\text{ multiplicity 3} \\ x=-3\text{ multiplicity 2} \\ \lim _(x\rightarrow\infty)(x-1)^3(x+3)^2=\infty \\ \lim _(x\rightarrow-\infty)(x-1)^3(x+3)^2=-\infty \end{gathered}`

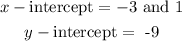
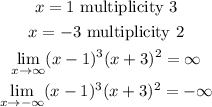
Explanation:

To find the x-intercepts factor the function to the simplest form:

`h(x)=(x-1)^3(x+3)^2`

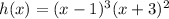
As we can see the zeros to the function would be 1 and -3, then its:

`\begin{gathered} x-\text{intercept}=-3\text{ and 1} \\ y-\text{intercept}=\text{ -9} \end{gathered}`

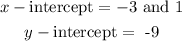
Zero has a "multiplicity", which refers to the number of times that its associated factor appears in the polynomial. Therefore, this function has multiplicity:

`\begin{gathered} x=1\text{ multiplicity 3} \\ x=-3\text{ multiplicity 2} \end{gathered}`

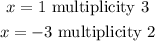
For the end behavior:

down/up

As x approaches infinity f(x) approaches infinity

As x approaches -infinity f(x) approaches -infinity

`\begin{gathered} \lim _(x\rightarrow\infty)(x-1)^3(x+3)^2=\infty \\ \lim _(x\rightarrow-\infty)(x-1)^3(x+3)^2=-\infty \end{gathered}`