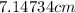Question

the length of a rectangle is 13 centimeters less then four times it’s width it’s area is 35 centimeters find the dimensions of the rectangle

Answer 1

The area of a recatngle is expressed as

`\begin{gathered} \text{Area of rectangle = L}* W \\ \text{where} \\ L\Rightarrow\text{length of the rectangle} \\ W\Rightarrow\text{ width of the rectangle } \end{gathered}`

Given that the length of the rectangle is 13 centimeters less than four times its width, this implies that

`L=4W-13\text{ ---- equation 1}`

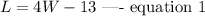
Tha area of the rectangle is 35 square centimeters. This implies that

`36=L* W\text{ --- equation 2}`

Substitute equation 1 into equation 2. Thus,

Solve equation 3 by using the quadratic formula expressed as

`\begin{gathered} W=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}_{} \\ \text{where} \\ a=4 \\ b=-13 \\ c=-36 \end{gathered}`

thus, we have

`\begin{gathered} W=\frac{-(-13)\pm\sqrt[]{(-13)^2-(4*4*-36)}}{2*4}_{} \\ =\frac{13\pm\sqrt[]{169+576}}{8} \\ =\frac{13\pm\sqrt[]{745}}{8} \\ =(13)/(8)\pm\frac{\sqrt[]{745}}{8} \\ =1.625\pm3.411836016 \\ \text{thus,} \\ W=5.036836016\text{ or W=}-1.786836016 \end{gathered}`

but the width cannot be negative. thus, the width of the recangle is

`W=5.036836016`

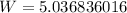
From equation 1,

`\begin{gathered} L=4W-13 \\ \end{gathered}`

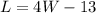
substitute the obtained value of W into equation 1.

Thus, we have

`\begin{gathered} L=4W-13 \\ =4(5.036836016)-13 \\ =20.14734-13 \\ \Rightarrow L=7.14734 \end{gathered}`

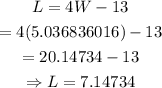
Hence:

The width is

`5.036836016cm`

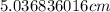
The length is

`7.14734cm`