In the first part of this problem, we must compute some statistic variables of two distributions:
0. the mean value,
,
1. the median,
,
2. the standard deviation.
,
3. the interquartile range.
1. The mean of a data set is the sum of all the data divided by the count n:
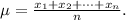
2. The median is the data value separating the upper half of a data set from the lower half, it is computed following these steps:
• arrange data values from lowest to the highest value,
,
• the median is the data value in the middle of the set
,
• if there are 2 data values in the middle the median is the mean of those 2 values.
3. The standard deviation for a sample data set is given by the following formula:
![\sigma=\sqrt[]{\frac{(x_1-\mu)^2+(_{}x_2-\mu)^2+\cdots+(x_n-\mu)^2}{n-1}_{}}\text{.}](https://img.qammunity.org/2023/formulas/mathematics/college/69l43wgi0bkmhv7is57h8i4vgvzp0irr6y.png)
4. The interquartile range (IQR) is given by:
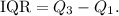
Where Q_1 and Q_3 are the first and third quartiles. The lowest quartile (Q1) covers the smallest quarter of values in your dataset.
--------------
Using the definitions above, we compute the mean, the median and the standard deviation for the samples taken by Manuel and Gretchen.
Manuel's sample
• Sample = {3, 6, 8, 11, 12, 8, 6, 3, 10, 5, 14, 9, 7, 10, 8}
,
• Count = 15
1. Mean
Using the formula above, we get:
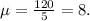
2. Median
We order the data set:
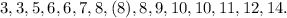
From the ordered data set, we see that the central number 8 divides the data set into two equal parts.
So the median of this sample is:
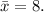
3. Standard deviation
Using the formula above, we get:
![\sigma=\sqrt[]{(138)/(15-1)}\cong3.14.](https://img.qammunity.org/2023/formulas/mathematics/college/80jc333fa108ttui4t7hc5zgcm6dzjgm8q.png)
4. Interquartile range
Dividing the data sample into quartiles, we have:
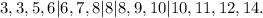
We have:
• Q_1 = 6,
,
• Q_3 = 10.
So the interquartile range is:
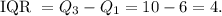
Gretchen's sample
• Sample = {22, 4, 7, 8, 12, 15, 10, 7, 9, 6, 13, 3, 8, 10, 10}
,
• Count = 15
1. Mean
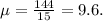
2. Median
We order the data set:
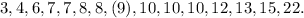
From the ordered data set, we see that the central number 8 divides the data set into two equal parts.
So the median of this sample is:
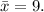
3. Standard deviation
![\sigma=\sqrt[]{(307.6)/(15-1)}\cong4.69.](https://img.qammunity.org/2023/formulas/mathematics/college/qzgzp6nhwtv0dmceta2e7tulw7e4yrrk7r.png)
4. Interquartile range
Dividing the data sample into quartiles, we have:
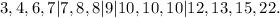
We have:
• Q_1 = 7,
,
• Q_3 = 12.
So the interquartile range is:
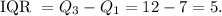
Answers
Manuel's sample
0. Mean = 8
,
1. Median = 8
,
2. Standard deviation ≅ 3.14
,
3. Interquartile range = 4
Gretchen's sample
0. Mean = 9.6
,
1. Median = 9
,
2. Standard deviation ≅ 4.69
,
3. Interquartile range = 5