As per given by the question,
There are given that, 4 green marbles and 1 blue marble contains in a box and pick a marble at randomly.
Now,
Here pick a marble out at random, so first pick a marble for blue;
Then,
Total number of green marbles is 4, and the total number of blue marble is 1, and;
The total numbers of marbles in a bag is, 4+1=5.
So,
For pick the blue marble from 5 marble,
Now,
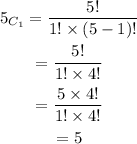
Now, for pick the green marble from 5 marbles.
Here, total green marble is 4.
So,
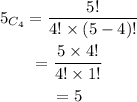
Now,
From the question, there are clearly mention that if pick a blue, then stop because you won 20 points.
So,
Probability of the blue marble that won the 20 points.
then,
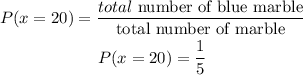
Now,
There are also mention that, pick a green marbles without replacing and if its blue then win the 10 points,
So,
probability of the blue marbles that won 10 pointss is,
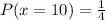
Now,
Here, find the probability that no points for the first green ball is,
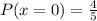
Now,
If you played this game 100 time, then the probability is,
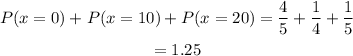
now,
For 100 times,
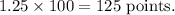
Hence, 125 points can you expect to win.