Question

match the system of equations with the solution set.hint: solve algebraically using substitution method.A. no solutionB. infinite solutionsC. (-8/3, 5)D. (2, 1)

Answer 1

We will solve all the systems by substitution method .

System 1.

By substituting the second equation into the first one, we get

`x-3((1)/(3)x-2)=6`

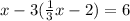
which gives

`\begin{gathered} x-x+6=6 \\ 6=6 \end{gathered}`

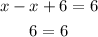
this means that the given equations are the same. Then, the answer is B: infinite solutions.

System 2.

By substituting the first equation into the second one, we have

`6x+3(-2x+3)=-5`

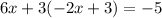
which gives

`\begin{gathered} 6x-6x+9=-5 \\ 9=-5 \end{gathered}`

but this result is an absurd. This means that the equations represent parallel lines. Then, the answer is option A: no solution.

System 3.

By substituting the first equation into the second one, we obtain

`-(3)/(2)x+1=-(3)/(4)x+3`

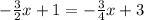
by moving -3/4x to the left hand side and +1 to the right hand side, we get

`-(3)/(2)x+(3)/(4)x=3-1`

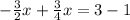
By combining similar terms, we have

`-(3)/(4)x=2`

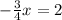
this leads to

`x=-(4*2)/(3)`

then, x is given by

`x=-(8)/(3)`

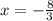
Now, we can substitute this result into the first equation and get

`y=-(3)/(2)(-(8)/(3))+1`

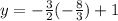
which leads to

`\begin{gathered} y=4+1 \\ y=5 \end{gathered}`

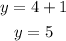
then, the answer is option C: (-8/3, 5)

System 4.

By substituting the second equation into the first one, we get

`-5x+(2x-3)=-9`

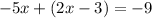
By combing similar terms, we have

`\begin{gathered} -3x-3=-9 \\ -3x=-9+3 \\ -3x=-6 \\ x=(-6)/(-3) \\ x=2 \end{gathered}`

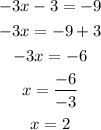
By substituting this result into the second equation, we have

`\begin{gathered} y=2(2)-3 \\ y=4-3 \\ y=1 \end{gathered}`

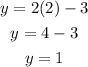
then, the answer is option D