Question

Mike had 28 books. His brother Joseph decided to give one third of his books to Mike. After that, Joseph and Mike had the exact same number of books. How many books did they have altogether?

Answer 1

Given the question in the question tab, the following are the solution step to get the number of books they have altogether.

Step 1: Write the notations for Joseph's and Mike's books

`\begin{gathered} \text{let j represents the number of books Joseph has,} \\ \text{let m represents the number of books Mike has} \end{gathered}`

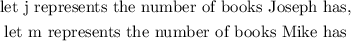
Step 2: Write the statements in a mathematical form

`\begin{gathered} m=28---\text{statement 1} \\ (1)/(3)of\text{ j was given to Mike to have }m+(j)/(3)=28+(j)/(3) \\ \text{After that, }28+(j)/(3)=(2j)/(3) \end{gathered}`

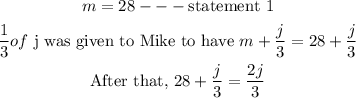
Step 3: Solve to get the value of j by using substitution method

`\begin{gathered} \\ m=28+(j)/(3) \\ 28+(j)/(3)=(2j)/(3) \\ \text{ multiply through by 3} \\ 84+j=2j \\ 84=2j-j \\ 84=j \\ j=84 \end{gathered}`

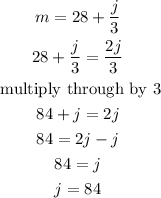
Therefore, Joseph had 84 books initially.

Step 4: Get the number of books they had altogether by summing the number of books for the each of them initially

`\begin{gathered} m=28,j=84 \\ \text{Total}=28+84=112 \end{gathered}`

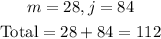
Hence, they both had 112 books altogether.