Answer:
The diameter of the base of the cylinder is 2 cm.
Step-by-step Step-by-step explanation:
GIVEN :
As per given question we have provided that :
- ➣ Height of cylinder = 14 cm
- ➣ Curved surface area = 88 cm²

TO FIND :
in the provided question we need to find :
- ➠ Radius of cylinder
- ➠ Diameter of cylinder

USING FORMULAS :
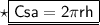

- ➛ Csa = Curved surface area
- ➛ π = 22/7
- ➛ r = radius
- ➛ h = height
- ➛ d = diameter

SOLUTION :
Firstly, finding the radius of cylinder by substituting the values in the formula :

Hence, the radius of cylinder is 1 cm.
———————————————————————
Now, finding the diameter of cylinder by substituting the values in the formula :

Hence, the diameter of the base of the cylinder is 2 cm.
