Question

Use the Rational Zeros Theorem to find all the real zeros of the polynomial function. Use the zeros to factor f over the real numbers. Hint solve this problem using P and Q's and synthetic division f(x) = x^3 + 2x^2 - 5x - 6A -3, -1, 2; f(x) = (x + 3)(x + 1)(x - 2)B-1; f(x) = (x + 1)(x2 + x - 6)C-3; f(x) = (x + 3)(x2 - x - 2)D-2, 1, 3; f(x) = (x + 2)(x - 1)(x - 3)

Answer 1

`f(x)=x^3+2x^2-5x-6`

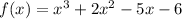
Since all coefficients are integers, we can apply the rational zeros theorem.

The trailing coefficient is -6 with the following factors (possible values for p):

`p\colon\pm1,\pm2,\pm3,\pm6`

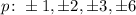
The leading coefficient is 1, with factors:

`q=\pm1`

Therefore, all the possible values of p/q are:

`(p)/(q)\colon\pm(1)/(1),\pm(2)/(1),\pm(3)/(1),\pm(6)/(1)`

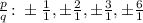
Simplifying, the possible rational roots are:

`\pm1,\pm2,\pm3,\pm6`

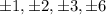
Next, we have to check if they are roots of the polynomials by synthetic division, in which the remainder should be equal to 0.

0. Dividing ,f (x), by ,x−1,. Remainder = ,-8, ,+1, is ,NOT ,a root.

,

1. Dividing ,f (x), by x+,1,. Remainder = 0, ,-1, ,IS ,a root.

,

2. Dividing ,f (x), by x-2. Remainder = 0, ,+2, ,IS ,a root.

,

3. Dividing ,f (x), by ,x+2,. Remainder = ,4, ,-2, is ,NOT ,a root.

,

4. Dividing ,f (x), by ,x−3,. Remainder = 24,, ,+3, is ,NOT ,a root.

,

5. Dividing ,f (x), by ,x+3,. Remainder = 0,, ,-3, IS ,a root.

,

6. Dividing ,f (x), by ,x−6,. Remainder = 252,, ,+6, is ,NOT ,a root.

,

7. Dividing ,f (x), by ,x+6,. Remainder = -120,, ,-6, is ,NOT ,a root.

Actual rational roots: A. -3, -1, 2; f(x) = (x + 3)(x + 1)(x - 2)