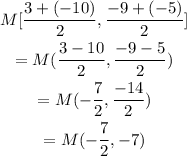Question

Find the midpoint of the line segment IJ where I (3,-9) and J (-10,-5)

Answer 1

M (-7/2, -7)

Step-by-step explanation:

Given the coordinates as I(3, - 9) and J(-10, -5), we can go ahead and determine the midpoint of the line segment IJ using the midpoint formula stated below;

`M((x_1+x_2)/(2),(y_1+y_2)/(2))`

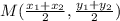
So we have that x1 = 3, x2 = -10, y1 = -9, and y2 = -5.

Let's go ahead and substitute the above values into our formula and simplify;

`\begin{gathered} M\lbrack(3+(-10))/(2),(-9+(-5))/(2)\rbrack \\ =M((3-10)/(2),(-9-5)/(2)) \\ =M(-(7)/(2),(-14)/(2)) \\ =M(-(7)/(2),-7) \end{gathered}`