Question

f(x) = x2 + 4 and g(x) = -x + 2Step 2 of 4: Find g(d) - f(d). Simplify your answer.Answer8(d) - f(d) =

Answer 1

`\begin{equation*} g(d)-f(d)=-d^2-d-2 \end{equation*}`

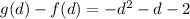
Step-by-step explanation:

Given:

`\begin{gathered} f(x)=x^2+4 \\ g(x)=-x+2 \end{gathered}`

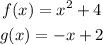
To find:

`g(d)-f(d)`

We can find g(d) by substituting x in g(x) with d, so we'll have;

`g(d)=-d+2`

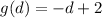
We can find f(d) by substituting x in f(x) with d, so we'll have;

`f(d)=d^2+4`

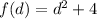
We can now go ahead and subtract f(d) from g(d) and simplify as seen below;

`\begin{gathered} g(d)-f(d)=(-d+2)-(d^2+4)=-d+2-d^2-4=-d^2-d+2-4 \\ =-d^2-d-2 \\ \therefore g(d)-f(d)=-d^2-d-2 \end{gathered}`

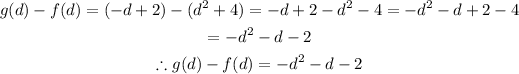
Therefore, g(d) - f(d) = -d^2 - d -2