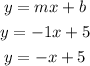The two points given are
A(-1, 6)
B(7, -2)
We shall start by calculating the slope of the line, since we've been given two points.
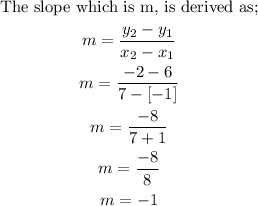
Next we shall derive the y-intercept, by inserting the known values into the equation in slope-intercept form.
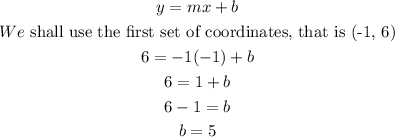
Having calculated the values of m (the slope) and b (the y-intercept), the equation is now;