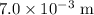Given:
The maximum current in the circuit is,
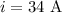
The power per length is,
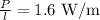
To find:
The diameter of the copper wire
Step-by-step explanation:
The power (P) produced by current i, through a copper wire of resistance R and length l is given by,
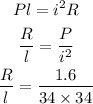
Now,

The resistivity of copper is,

So, we can write,
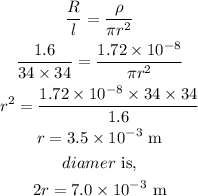
Hence, the diameter is,