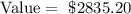The volume of a right rectangular prism is given by
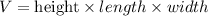
From the given information, we know that
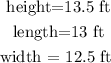
So, the volume is given by
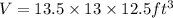
which gives
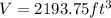
Now, since the content weigh 0.18 pound per cubic foot and worth $7.18 per pound, the value of the container is given by,
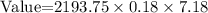
Therefore, by rounding to the nearest cent, the answer is: