Answer:
Given:
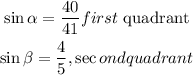
Step 1:
Figure out the value of cos alpha
We will use the Pythagoras theorem below
![\begin{gathered} \text{hyp}^2=\text{opp}^2+\text{adj}^2 \\ \text{hyp}=41,\text{opp}=40,\text{adj}=x \\ 41^2=40^2+x^2 \\ 1681=1600+x^2 \\ x^2=1681-1600 \\ x^2=81 \\ x=\sqrt[]{81} \\ x=9 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/901c4g8qi3wncnkufq6d8ciulq2keucsvs.png)
Hence,
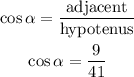
Step 2:
Figure out the value of cos beta
To figure this out, we will use the Pythagoras theorem below
![\begin{gathered} \text{hyp}^2=\text{opp}^2+\text{adj}^2 \\ \text{hyp}=5,\text{opp}=4,\text{adj}=y \\ 5^2=4^2+y^2 \\ 25=16+y^2 \\ y^2=25-16 \\ y^2=9 \\ y=\sqrt[]{9} \\ y=3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zk3q73tp8a01cfirveza8dek3oq1ubdhgh.png)
Hence,
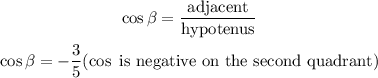
Step 3:
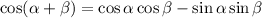
By substituting the values, we will have
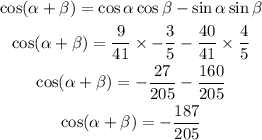
Hence,
The final answer = -187/205