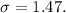For this type of problem we use the following formula:
![\begin{gathered} \sigma=\sqrt[]{\frac{\sum^{}_{}(x_i-\mu)^2}{N},} \\ \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/eiirpnlry0v3g6kfyv7owdntbrtqriliol.png)
where μ is the population mean, xi is each value from the population, and N is the size of the population.
First, we compute the population mean in order to do that we use the following formula:
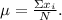
Substituting each value of x_i in the above formula we get:
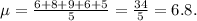
Now, we compute the difference of each x_i with the mean:
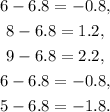
Squaring each result we get:
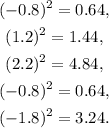
Now, we add the above results:
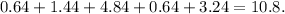
Dividing by N=5 we get:
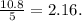
Finally, taking the square root of 2.16 we obtain the standard deviation,
![\sigma=\sqrt[]{2.16}\approx1.47.](https://img.qammunity.org/2023/formulas/mathematics/college/ktdve2fsc99hmhe7aqi45qx3dblmbsmo0t.png)
Answer: