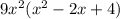Given the expression:
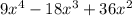
You can factor it by following these steps:
1. Find the Greatest Common Factors (GCF) of the terms:
- The Greatest Common Factor (GCF) of the coefficients can be found by decomposing each coefficient into their Prime Factors:
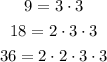
Notice that all the coefficients have:

Therefore, that is the Greatest Common Factor (GCF) of the coefficients.
- The Greatest Common Factor (GCF) of the variables is the variable with the lowest exponent:
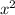
Hence:
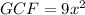
2. Now you can factor it out:

Hence, the answer is: