Question

Factor the following polynomials completely.(x + y)³ + 1 =

Answer 1

Given the equation (x + y)³ + 1 , we can assume we have two terms here. These are (x + y)³ and 1. Since both terms are perfect cubes, we can use the sum of cubes formula which is:

`a^3+b^3=(a+b)(a^2-ab+b^2)`

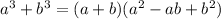
where a = (x+y) and b = 1.

Therefore, the factors of (x + y)³ + 1 is:

`\begin{gathered} \mleft(x+y\mright)^3+1=(x+y+1)\lbrack(x+y)^2-(x+y)(1)+1^2) \\ (x+y)^3+1=(x+y+1)(x^2+2xy+y^2-x-y+1) \end{gathered}`

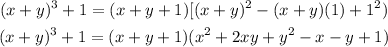
The factor of (x + y)³ + 1 is (x + y + 1)(x² + 2xy + y² - x - y +1).