To answer this question, we need to know that two linear equation that does not have solutions must not cross to each other, that is, they do not have a common point. For this case, both lines must be parallel lines. So in the question, we need to find a parallel line to the given line. Two parallel lines have the same slope.
Then, we have that the line must pass through (12, 7), and, because it is parallel to y = -3/4x + 8, and the slope for this line is m = -3/4, then, the line equation is, applying the point-slope form of the line:

And
x1 = 12
y1 = 7
m = -3/4
Then
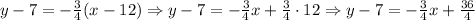
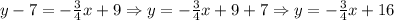
Then, the line equation is y = -3/4 x + 16.
We can check this if we use the elimination method as follows:
This is a FALSE result, and we do not have solutions for this system. Therefore, the line equation is y = -3/4 x + 16.