Question

An accountant finds that the gross income, in thousands of dollars, of a small business can be modeled by the polynomial −0.3t 2 + 8t + 198, where t is the number of years after 2010. The yearly expenses of the business, in thousands of dollars, can be modeled by the polynomial −0.2t 2 + 2t + 131.a. Find a polynomial that predicts the net profit of the business after t years. b. Assuming that the models continue to hold, how much net profit can the business expect to make in the year 2016?I know that the equation is -0.1t^2+6t+67, but i don't know how to find part b.

Answer 1

Explanation:

a.

We know that the net profit is equal to the incomes minus the expenses, therefore, the final equation would be:

`\begin{gathered} \text{profit = income - expense} \\ \text{replacing} \\ p=-0.3t^2+8t+198-(-0.2t^2+2t+131) \\ p=-0.3t^2+8t+198+0.2t^2-2t-131 \\ p=-0.1t^2+6t+67 \end{gathered}`

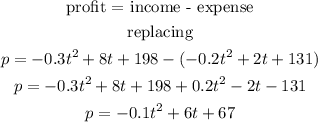
b. t is the number of the years after 2010. Therefore, for the year 2016, x is equal to 6 (2016 - 2010), we replace: