Question

A spring with spring constant 40 N/m is compressed .1m past it natural length. A mass of .5kg is attached to the spring. A. What is the elastic potential energy stored in the spring?B. The spring is released. What is the speed of the masses as it reaches the natural length of the spring?

Answer 1

Given data

*The given spring constant is k = 40 N/m

*The given compressed length is x = 0.1 m

*The given mass is m = 0.5 kg

(a)

The formula for the elastic potential energy stored in the spring is given as

`U_p=(1)/(2)kx^2`

Substitute the values in the above expression as

`\begin{gathered} U_p=(1)/(2)(40)(0.1)^2 \\ =0.2\text{ J} \end{gathered}`

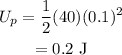
Hence, the elastic potential energy stored in the spring is 0.2 J

(b)

The formula for the speed of the masses is given by the conservation of energy as

`\begin{gathered} U_p=U_k \\ (1)/(2)kx^2=(1)/(2)mv^2 \\ v=x\sqrt[]{(k)/(m)} \end{gathered}`

Substitute the values in the above expression as

`\begin{gathered} v=(0.1)\sqrt[]{(40)/(0.5)} \\ =0.89\text{ m/s} \end{gathered}`

Hence, the speed of the masses as it reaches the length of the spring is v = 0.89 m/s