Given data:
* The mass of the motorcycle is m = 244 kg.
* The speed of the motorcycle is u = 14.7 m/s.
Solution:
(A). The kinetic energy of the motorcycle is,
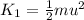
Substituting the known values,

Thus, the value of kinetic energy is 26362.98 J.
(B). If the speed of the motorcycle is increased by a factor of 1.6,
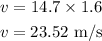
Thus, the kinetic energy of the motorcycle becomes,
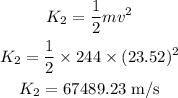
Dividing K_2 by K_1,
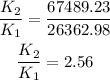
Thus, the kinetic energy is increased by the factor of 2.56.
(C). The 1/3 of the kinetic energy in the first part is,
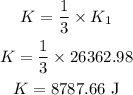
Thus, the speed of the motorcycle with the kinetic energy K is,
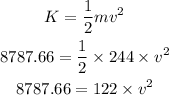
By simplifying,
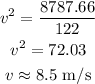
Thus, the speed of the motorcycle is 8.5 m/s.