We have the following triangles:
And we need to determine if they are similar by identifying the similarity statement.
To determine that similarity statement, we can proceed as follows:
1. Check the measures of the internal angles of the triangles. We need to remember that the sum of the internal angles of a triangle is 180 degrees. Then we have:
2. We can see that to find the angles in the first triangle, EFG, and in the second triangle, JKL, we have that the sum of the three angles must be 180 degrees, and we obtained the other angles as follows:
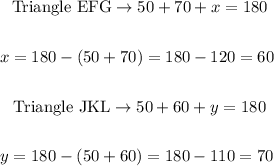
3. Then we can redraw the triangles as follows:
4. Now, since we can see that, at least, two of the angles of the triangles are congruent (then the third one is also congruent, that is, has the same measure), we also have that to prove that if two triangles are similar it is sufficient that two of the corresponding angles of one triangle are congruent to the two corresponding angles of the other triangle, and this is known as the Angle-Angle method for proving similar triangles, then we can conclude that:
Triangle EFG is similar to triangle JKL by the Angle-Angle method.
Therefore, in summary, we have that:
Triangle EFG is similar to Triangle JKL by Angle-Angle similarity
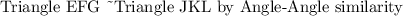
[Last option]