In a parallelogram, the opposite sides are parallel.
This means that RS is parallel to OT. So, the y value of S is the same as the y value of R, which is d, so y = d. Thus:
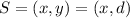
Now, we need to find x.
Since the sides RO and ST are also parallel, the x distance from O to R is the same as the x distance from T to S.
The x distance from O to R is
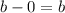
The x distance from T to S is
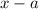
Since these x distances are equal, then:
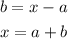
Then, the coordinates of S are:
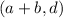
Which corresponds to option B.