Given:
• A = 100 degrees
,
• a = 3.5
,
• b = 3
Let's solve for the remaining angles and side of the triangle.
Here, we are given one angle and two sides.
To solve, apply the Law of Sines:
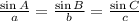
• To solve for measure of angle B, we have:
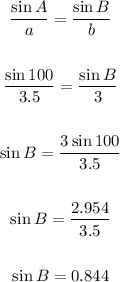
Take the sine inverse of both sides:
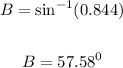
Therefore, the measue of angle B is = 57.58 degrees.
• To solve for angle C, apply the Triangle Angle Sum Theorem.
m∠A + m∠B + m∠C = 180
m∠C = 180 - m∠A - m∠B
m∠C = 180 - 100 - 57.68
m∠C = 22.32
The measure of angle C is 22.32 degrees.
• To find the length of c, apply the Law of Sines:
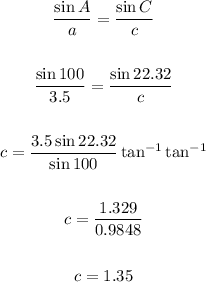
The length of side c is 1.35 units.
ANSWER:
• B = 57.58,°
,
• C = 22.32,°
,
• c = 1.35