The angle between the components x and y of a vector is given by:
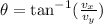
once we know this we need to find in which quadrant the vector lies so we know how to calculate the correct direction.
Vector A lies in the fourth quadrant this means that we need to subtract theta to 360° in order to get the direction of the vector, then we have:
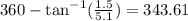
Therefore the direction of vector A is 343.61°
Vector B lies in the second quadrant, this means that we need to subtract theta (given by the first equation) to 180° in order to get the direction, then we have:
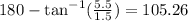
Therefore the direction of vector B is 105.26°
Let's find vector A+B:
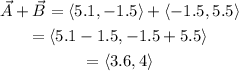
Then we have that:
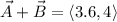
To find its magnitude we have to remember that the magnitude of any vector is given by:
![\lvert\vec{v}\rvert=\sqrt[]{v^2_x+v^2_y}](https://img.qammunity.org/2023/formulas/physics/college/ot5idls7j4j85y6det7jrloscseboz1g8l.png)
Then for vector A+B we have:
![\begin{gathered} \lvert\vec{A}+\vec{B}\rvert=\sqrt[]{(3.6)^2+(4)^2} \\ =5.38 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/fxiyhqd6hu62wj9h5saw8xne5g41vczbbu.png)
Therefore the magnitude of vector A+B is 5.38 meters.
Vector A+B lies in the first quadrant, then its direction is given by the expression for theta, then we have:
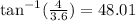
Therefore the direction of vector A+B is 48.01°