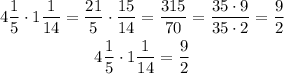Question

7 1/3 × 2 2/11 3/5 × 6 2/34 1/5 × 1 1/14

Answer 1

It is easier to perform the operations if you convert the mixed fractions into improper fractions.

For point 1. Make the mixed fractions improper first

`7(1)/(3)=(3\cdot7+1)/(3)=(21+1)/(3)=(22)/(3)`
`2(2)/(11)=(11\cdot2+2)/(11)=(22+2)/(11)=(24)/(11)`

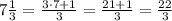
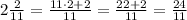
Now, the multiplication of fractions is done like this

`(a)/(b)\cdot(c)/(d)=(a\cdot c)/(b\cdot d)`

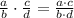
Then, you have

`7(1)/(3)\cdot2(2)/(11)=(22)/(3)\cdot(24)/(11)=(528)/(33)=16`

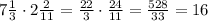
For point 2.

`6(2)/(3)=(3\cdot6+2)/(3)=(18+2)/(3)=(20)/(3)`

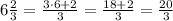
Now multiplying the improper fractions you have

`(3)/(5)\cdot6(2)/(3)=(3)/(5)\cdot(20)/(3)=(60)/(15)=4`

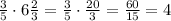
Finally for point 3.

`4(1)/(5)=(5\cdot4+1)/(5)=(20+1)/(5)=(21)/(5)`
`1(1)/(14)=(14\cdot1+1)/(14)=(14+1)/(14)=(15)/(14)`

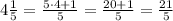
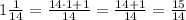
Now multiplying the improper fractions you have

`\begin{gathered} 4(1)/(5)\cdot1(1)/(14)=(21)/(5)\cdot(15)/(14)=(315)/(70)=(35\cdot9)/(35\cdot2)=(9)/(2) \\ 4(1)/(5)\cdot1(1)/(14)=(9)/(2) \end{gathered}`