Question

Transform AABC by the following transformations:• Reflect across the line y = -X• Translate 1 unit to the right and 2 units down.87BА )5421-B-7-6-5-4-301245678- 1-2.-3-5-6-7-8Identify the final coordinates of each vertex after both transformations:A"B"(C"

Answer 1

A reflection on the line y = -x is gotten as

`y=-x\colon(x,y)\rightarrow(-y,-x)`

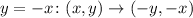
So, the coordinates of points A, B and C are

A(3, 6)

B(-2, 6)

C(3, -3)

Traslating this becomes

`\begin{gathered} A\mleft(3,6\mright)\rightarrow A^(\prime)(-6,-3) \\ B(-2,6)\rightarrow B^(\prime)(-6,2) \\ C(3,-3)\rightarrow C^(\prime)(3,-3 \end{gathered}`

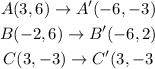
Now translate 1 unit to the right and 2 units down becomes

`\begin{gathered} A^(\prime)(-6,-3)\rightarrow A^(\doubleprime)(-5,-5) \\ B^(\prime)(-6,2)\rightarrow B^(\doubleprime)(-5,0) \\ C^(\prime)(3,-3\rightarrow C^(\doubleprime)(4,-5) \end{gathered}`

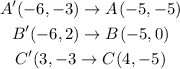
So, I will attach an image now to show you the final translation.