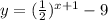
First, we can start input small whole numbers in the function to see if we get a whole number. Let's try with 0, 1 and 2:
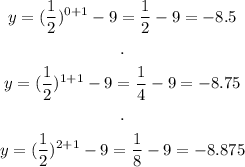
None of those values worked. Let's try negative integers, such as -1 and -2:

We get integer coordinates if we use negative integers. Then, we need at least 5 points. Let's use x = -1, -2, -3, -4, -5
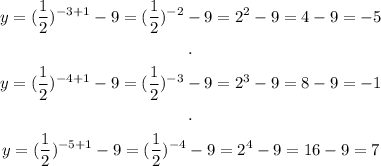
We have the points:
(-1, -8), (-2, -7), (-3, -5), (-4, -1) and (-5, 7)
If we locate them in the cartesian plane:
And now, we can estimate the graph. An exponential function where the base is smaller than 1, describes an exponential decay, and the term "-9" is applying a shift 9 units down, and also y = -9 is a horizontal asymptote. With all this and the points we just found: