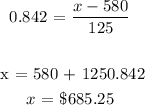Question

Suppose that the balance of a person’s bank account in US is normally distributed with mean $580 and standard deviation $125. Find the amount of money which would guarantee a person has more money in their account than 80% of US residents.I want an answer and explanation.

Answer 1

`\text{ \$685.25}`

Step-by-step explanation:

Here, we want to get the amount of money that would guarantee that a person has more money than 80%

That means the probability is greater than 80% or 0.8

Thus, we need to get the z-score that corresponds to this probability

Using a z-score table, we can get this as follows:

`P(x\text{ }>\text{z\rparen= 0.842}`

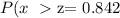
We will now get the value from the obtained z-score

Mathematically:

`\begin{gathered} z\text{ = }(x-\mu)/(\sigma) \\ \\ \text{ x is the value we want to calculate} \\ \mu\text{ is the mean} \\ \sigma\text{ is the standard deviation} \end{gathered}`

Substituting the values, we have it that:

`\begin{gathered} 0.842\text{ = }(x-580)/(125) \\ \\ \text{ x = 580 + 125\lparen0.842\rparen} \\ x\text{ = \$685.25} \end{gathered}`