Question

Prealgebra- Write an equation of the line that passes through the points(Question in photo) (Can only attach one photo at time, so for graphing part of question, i will send the photo)

Answer 1

Given:

Point 1 → (-5, 0.6)

Point 2 → (5, -2.4)

Find: the equation of the line and its graph

Solution:

To help us determine the equation of the line passing through the given points, let's use the Two-Point Form formula.

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

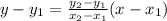
Let's plug into the formula above the coordinates of the two points.

`y-0.6=(-2.4-0.6)/(5-(-5))(x-(-5))`

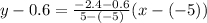
Then, solve.

`y-0.6=(-3)/(10)(x+5)`

Multiply -3/10 by the terms inside the parenthesis.

`y-0.6=-(3)/(10)x-1.5`

Add 0.6 on both sides of the equation.

`y-0.6+0.6=-(3)/(10)x-1.5+0.6`
`\begin{gathered} y=-(3)/(10)x-0.9 \\ or \\ y=-0.3x-0.9 \end{gathered}`

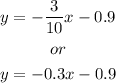
Hence, the equation of the line passing through the given points in slope-intercept form is y = -0.3x - 0.9.

In the equation, the slope is -3/10 while the y-intercept is -0.9.

Since the slope is negative, the line must be leaning to the left. Since the y-intercept is -0.9, the line must cross the y-axis or the vertical line at -0.9. Hence, the graph of the equation is: