SOLUTION
To solve this we will use the form for exponential growth to determine the formula to use.
Exponential growth has the form

Now the frogs tripple in population after 9 days. Initially they were 21. So in 9 days they become
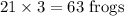
Applying the formula, we have
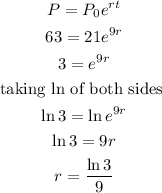
The time for the frogs to get to 290 becomes
![undefined]()