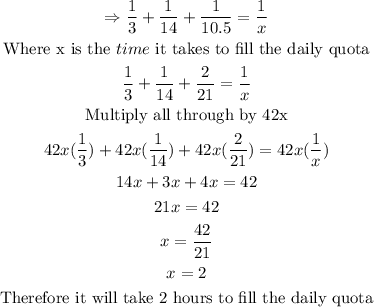Question

A local dairy has three machines to fill half-gallon milk cartons. The machines can fill the daily quota in 3 hrs, 14 hrs, and 10.5 hrs, respectively. Find how long it takes to fill the daily quota if all three machines are running.

Answer 1

It will take 2 hours to fill the daily quota if all the machines are running.

Step-by-step explanation

To find how long it takes to fill the daily quota if all the machines are running, we use the relation below:

Rate of machine 1 + Rate of machine 2 + Rate of machine 3 = Total rate of the machines

`\begin{gathered} \Rightarrow(1)/(3)+(1)/(14)+(1)/(10.5)=(1)/(x) \\ \text{Where x is the }time\text{ it takes to fill the daily quota} \\ (1)/(3)+(1)/(14)+(2)/(21)=(1)/(x) \\ \text{Multiply all through by 42x} \\ 42x((1)/(3))+42x((1)/(14))+42x((2)/(21))=42x((1)/(x)) \\ 14x+3x+4x=42 \\ 21x=42 \\ x=(42)/(21) \\ x=2 \\ \text{Therefore it will take 2 hours to fill the daily quota} \end{gathered}`