Question

A computer retail store has 10 personal computers in stock. A buyer wants to purchase 4of them. Unkown to either the retail store or the buyer, 4 of the computers in stock have defective hard drives. Assume that the computers are selected at random.A. In how many different ways can the 4 computers be chosen?Answer: 210B. What is the probability that exactly one of the computers will be defective?Answer:

Answer 1

A.

The number of different ways the computers can be chosen is given by a combination of 10 choose 4.

A combination of n choose p is given by the formula below:

`C(n,p)=(n!)/(p!(n-p)!)`

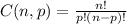
So we have:

`C(10,4)=(10!)/(4!(10-4)!)=(10\cdot9\cdot8\cdot7\cdot6!)/(4\cdot3\cdot2\cdot6!)=210`

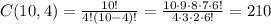
B.

If the first computer chosen is the one defective, the probability of the first PC being defective is 4/10, the probability of the second one not being defective will be 6/9, for the third not being defective is 5/8 and for the fourth not being defective is 4/7.

Since the defective PC can be any of the 4 bought, we need to multiply the probability above by 4. So the final probability is:

`P=4\cdot(4)/(10)\cdot(6)/(9)\cdot(5)/(8)\cdot(4)/(7)=0.3809`