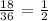Answer:
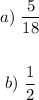
Step-by-step explanation:
Here, we want to compute some probabilities
The first thing to do is to get the count of results in our sample space
In the sample space, the total possible results is 36
Now, let us get the probabilities
a) The event that the sum is greater than 8
We have to count possible results greater than 8 here
3, 6 (3 on the first die, 6 on the second)
6,3 (6 on the first die, 3 on the second)
6,4 (6 on the first die, 4 on the second)
4,6
4,5
5,4
5,5
5,6
6,5
6,6
The number of possible results greater than 8 is 10
Thus, we have the probability as the count of this divided by the total number of possible results
Mathematically, we have that as:
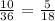
b) The sum is an odd number
For the sum to be an odd number, we know that if we add a table of 6 rows for all the sums, the even sum on each line is 3
The total even sum is 6 * 3 = 18
The probability is thus: