Question

Find the center, vertices, foci, endpoints of the latera recta and equations of the directrices. Then sketch the graph of the ellipse.

Answer 1

The given equation of ellipse is,

`((x-2)^2)/(16)+(y^2)/(4)=1\text{ ---(1)}`

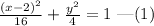
The above equation can be rewritten as,

`((x-2)^2)/(4^2)+(y^2)/(2^2)=1\text{ ----(2)}`

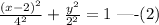
The above equation is similar to the standard form of the ellipse with center (h, k) and major axis parallel to x axis given by,

`((x-h)^2)/(a^2)+(y^2)/(b^2)=1\text{ ----(3)}`

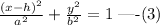
where a>b.

Comparing equations (2) and (3), h=2, k=0, a=4 and b= 2.

Hence, the center of the ellipse is (h, k)=(2, 0).

The coordinates of the vertices are given by,

`\begin{gathered} (h+a,\text{ k)=(2+}4,\text{ }0)=(6,\text{ 0)} \\ (h-a,\text{ k)=(2-}4,\text{ }0)=(-2,\text{ 0)} \end{gathered}`

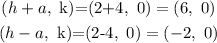
Hence, the coordinates of the vertices are (6, 0) and (-2,0).

The coordinates of the co-vertices are given by,

`\begin{gathered} (h,\text{ k+}b)=(2,\text{ }0+2)=(2,\text{ 2)} \\ (h,\text{ k-}b)=(2,\text{ }0-2)=(2,\text{ -2)} \end{gathered}`

Hence, the coordinates of the co-vertices are (2, 2) and (2, -2).

The coordinates of the foci are (h±c, k).

`\begin{gathered} c^2=a^2-b^2 \\ c^2=4^2-2^2 \\ c^2=16-4 \\ c^2=12 \\ c=2\sqrt[]{3} \end{gathered}`

Using the value of c, the coordinates of the foci are,

`\begin{gathered} \mleft(h+c,k\mright)=(2+2\sqrt[]{3},\text{ 0)} \\ (h-c,k)=(2-2\sqrt[]{3},\text{ 0)} \end{gathered}`

Therefore, the coordinates of the foci are,

`(2+2\sqrt[]{3},\text{ 0) and }(2-2\sqrt[]{3},\text{ 0)}`

The endpoints of the latus rectum is,

`\begin{gathered} (h+c,\text{ k}+(b^2)/(a))=(2+2\sqrt[]{3},\text{ 0+}\frac{2^2}{4^{}}) \\ =(2+2\sqrt[]{3},\text{ 1)}^{} \\ (h-c,\text{ k}+(b^2)/(a))=2-2\sqrt[]{3},\text{ 0+}\frac{2^2}{4^{}}) \\ =(2-2\sqrt[]{3},\text{ 1}^{}) \\ (h+c,\text{ k-}(b^2)/(a))=(2+2\sqrt[]{3},\text{ 0-}\frac{2^2}{4^{}}) \\ =(2+2\sqrt[]{3},\text{ -1}^{}) \\ (h-c,\text{ k-}(b^2)/(a))=(2-2\sqrt[]{3},\text{ 0-}\frac{2^2}{4^{}}) \\ =(2-2\sqrt[]{3},\text{ -1}^{}) \end{gathered}`

Therefore, the coordinates of the end points of the latus recta is,

`(2+2\sqrt[]{3},\text{ 1)},\text{ }(2-2\sqrt[]{3},\text{ 1}^{}),\text{ }(2+2\sqrt[]{3},\text{ -1}^{})\text{ and }(2-2\sqrt[]{3},\text{ -1}^{})`

Now, the equations of the directrices is,

`\begin{gathered} x=h\pm(a)/(e) \\ x=\pm\frac{a}{\sqrt[]{1-(b^2)/(a^2)}} \\ x=2\pm\frac{4}{\sqrt[]{1-(2^2)/(4^2)}} \\ x=2\pm\frac{4}{\sqrt[]{1-\frac{1^{}}{4^{}}}} \\ x=2\pm\frac{4}{\sqrt[]{(3)/(4)^{}}} \\ x=2\pm4\sqrt[]{(4)/(3)} \end{gathered}`

Here, e is the eccentricity of the ellipse.

Therefore, the directrices of the ellipse is

`x=2\pm4\sqrt[]{(4)/(3)}`

Now, the graph of the ellipse is given by,